Imaginad que tenemos un programa que queremos emitir por la radio. Este programa podría ser una canción, o un partido de fútbol, o un noticiero, o lo que sea. El programa puede ser en directo, o puede estar grabado en una cinta o en un CD o en un MP3. En todo caso, el programa se compone de ondas sonoras que queremos convertir en ondas de radio para que la gente pueda recibirlas y escuchar el programa en sus casas.
Obviamente, esto no es tan sencillo como enchufar directamente el micrófono o el reproductor de MP3 a la antena emisora. Si esto pudiese funcionar, sólo podría haber una emisora de radio en cada sitio. Además, las ondas de radio no se transmiten nada bien a las frecuencias de las ondas sonoras; para una buena transmisión, las ondas de radio necesitan tener frecuencias de cientos de miles o millones de ciclos por segundo. Por lo tanto, es necesario un proceso para convertir las ondas sonoras de baja frecuencia en ondas de radio de alta frecuencia; este proceso se llama modulación.
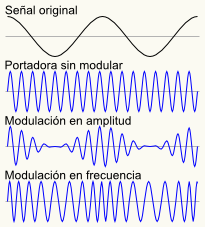
Hay muchos sistemas de modulación, pero los más conocidos, por ser utilizados en la radio comercial, son AM y FM. La idea general con los dos sistemas es que la emisora produce una onda de una frecuencia determinada (onda portadora), cuyas propiedades varían según varía la amplitud de la onda sonora correspondiente al programa a emitir. Por ejemplo, en la modulación en amplitud (AM), la amplitud de la portadora varía según la magnitud de la onda sonora; en cambio, en modulación en frecuencia (FM), la amplitud es constante y lo que varía es la frecuencia.
Es bastante fácil demodular una señal de radio modulada en amplitud. De hecho, es posible fabricar un receptor de radio AM con nada más que un cable de varios metros de largo, una conexión a tierra, un circuito resonante (compuesto por una bobina y un condensador), un diodo y un auricular. En este tipo de radio, la antena capta las señales, el circuito resonante amplifica las señales correspondientes a la frecuencia de resonancia, el diodo rectifica la señal oscilante para extraer la señal original, y el auricular la convierte en sonido. Este es el principio del funcionamiento de la radio de galena, o de las radios que se fabricaban los soldados durante la segunda guerra mundial utilizando una hoja de afeitar y un lápiz como diodo.
El problema de AM es que es bastante susceptible a los ruidos y a las interferencias, ya que un cambio en la amplitud de la señal de radio provoca un cambio en el sonido tras la demodulación. FM, en cambio, es más resistente a éstos, ya que el receptor de radio se aferra a la señal más fuerte (efecto captura) y es más difícil que una interferencia supere en potencia a la señal de radio, a menos que ésta no sea muy potente.
En el artículo anterior hablé de cómo funciona un descodificador de TDT, y dije que muchos descodificadores USB, basados en el chip RTL2832U, tienen una función que permite sintonizar una frecuencia y capturar las señales de radio que se reciben en esa frecuencia. Así, el ordenador recibe unos cuantos millones de muestras por segundo, cada muestra compuesta por dos bytes que representan la parte real e imaginaria de un número complejo. Este número complejo es el resultado de “multiplicar” la señal recibida en la antena por \(e^{-i2\pi f_c t}\) (donde \(f_c\) es la frecuencia a sintonizar), pasar el resultado por un filtro paso bajo para evitar aliasing, y pasar este resultado por un conversor analógico-digital que produce números entre 0 y 255 que representan las distintas magnitudes de las señales entre -1 y 1.
En resumen: el descodificador nos da números complejos entre \(-1-i\) y \(1+i\) que representan señales de radio. Cada segundo recibimos un par de millones de estos números, y si escribimos software para demodular señales de radio en tiempo real, este software tiene que funcionar rápido para no quedarse atrás.
Como comenté, hice una aplicación para escuchar radio AM y FM en el navegador Chrome. Esta aplicación está escrita en JavaScript, que no es precisamente el lenguaje que uno elegiría para escribir aplicaciones de proceso de señales en tiempo real, pero yo lo elegí para ver si sería capaz de hacerlo funcionar (spoiler: sí, fui capaz). En el resto de este artículo voy a explicar cómo se demodulan señales AM y FM. Me temo que tiene que haber cierta cantidad de fórmulas matemáticas, pero voy a tratar de explicarlo bien.
Para comenzar, vamos a imaginar una emisora de radio que está transmitiendo una portadora de amplitud y frecuencia constantes. Supongamos que la amplitud es \(A\) y la frecuencia es \(f_c\). Nos da igual cuáles son los valores de \(A\) y \(f_c\), excepto que \(f_c\) es un número de ciclos por segundo bastante alto (cientos de miles o millones de ciclos por segundo) y que tenemos un filtro paso bajo que bloquea \(f_c\). Este filtro puede estar en el descodificador o puede estar implementado en software; nos da totalmente igual. El caso es que cualquier frecuencia \(f_c\) o mayor que \(f_c\) queda bloqueada.
La portadora transmitida por esta emisora es una senoidal que se puede representar matemáticamente mediante la fórmula \(A\cos(2\pi f_c t + \varphi)\). Esto se lee como una senoidal real de amplitud \(A\), frecuencia \(f_c\) ciclos por segundo (o \(2\pi f_c\) radianes por segundo) y fase \(\varphi\). Si recordáis mis artículos anteriores, sabréis que una senoidal real es la suma de dos ondas complejas, una con frecuencia positiva y otra con frecuencia negativa. Por lo tanto, esta portadora también se puede representar como \(\frac{A}{2}e^{-i(2\pi f_c t + \varphi)} + \frac{A}{2}e^{i(2\pi f_c t + \varphi)}\). Es decir, una onda compleja de amplitud \(\frac{A}{2}\), frecuencia \(-f_c\) ciclos por segundo y fase \(-\varphi\) sumada a otra onda compleja de la misma amplitud, frecuencia \(f_c\) y fase \(\varphi\).
Ahora imaginemos que traemos nuestro descodificador de TDT y sintonizamos esa portadora. Para sintonizar una señal de frecuencia \(f_c\), el sintonizador multiplica la señal recibida en la antena por una onda compleja de frecuencia \(-f_c\). La fórmula de esta onda compleja es \(e^{-i2\pi f_c t}\). Como resultado, a cada una de las dos componentes de la portadora original se le resta la frecuencia \(f_c\), con lo que queda una componente de frecuencia \(-2f_c\) y fase \(-\varphi\) y otra componente de frecuencia \(0\) y fase \(\varphi\). Matemáticamente hablando, el resultado es \(\frac{A}{2}e^{-i(2\pi 2f_c t + \varphi)} + \frac{A}{2}e^{i\varphi}\). Ahora bien, esta señal resultante pasa a continuación por un filtro paso bajo cuya frecuencia umbral es menor que \(f_c\), por lo que la componente de frecuencia \(-2f_c\) queda bloqueada y sólo pasa la componente de frecuencia \(0\), dando como resultado un número constante \(\frac{A}{2}e^{i\varphi}\). Es decir: todas las muestras son números complejos de valor absoluto \(\frac{A}{2}\) y ángulo \(\varphi\).
Ahora podemos imaginar qué ocurre si, en lugar de transmitir una señal de amplitud constante, la emisora transmite una señal de amplitud variable. Esta amplitud la podemos representar mediante la función \(m(t)\). Para calcular qué es lo que se recibe en el descodificador podemos realizar los mismos cálculos de antes, pero donde ponía \(A\) ahora ponemos \(m(t)\), con lo que el resultado es \(\frac{m(t)}{2}e^{i\varphi}\). Es decir, todas las muestras son números complejos de valor absoluto \(\frac{m(t)}{2}\) y ángulo \(\varphi\). Como \(m(t)\) varía con el tiempo, el valor absoluto de las muestras también varía con el tiempo, y para obtener el valor de \(m(t)\) no tenemos más que calcular el valor absoluto de cada muestra y multiplicarlo por 2: \(m(t) = 2|s(t)|\).
En un sistema de modulación AM, este es precisamente el tipo de señal que una emisora transmite, así que podemos utilizar los cálculos de arriba para ver cómo demodular una señal AM. En AM, el valor de \(m(t)\) es una transformación matemática del programa que se está emitiendo. Se define esta función como \(m(t) = \frac{1}{2}(1 + p(t))\), donde \(p(t)\) es una función que representa el programa que se quiere emitir. De este modo, \(m(t)\) varía entre 0 y 1 según \(p(t)\) varía entre -1 y 1. Despejando para obtener \(p(t)\) a partir de \(m(t)\) tenemos que \(p(t) = 2m(t) - 1\), por lo tanto, para calcularlo a partir de las muestras recibidas no hay más que calcular \(p(t) = 4|s(t)| - 1\).
Es decir, para demodular una señal transmitida usando AM tenemos que obtener el valor absoluto de cada muestra, multiplicarlo por 4 y restarle 1. Suponiendo que no hubiera interferencias o atenuación, el resultado sería la onda sonora original. En la práctica casi siempre hay algo de ruido en la señal, y siempre hay atenuación. Para evitar los efectos de la atenuación, lo que hace mi programa es medir la intensidad de la señal recibida y ajustar los números que se multiplican y suman al valor absoluto de la señal recibida. De este modo, la señal siempre se oye alta.
En una señal FM, como dije antes, la amplitud es constante pero la frecuencia varía. Existe una frecuencia central \(f_c\) y una frecuencia de desviación máxima \(f_\Delta\). La frecuencia de la portadora varía continuamente entre \(f_c-f_\Delta\) y \(f_c+f_\Delta\), dependiendo del valor de \(p(t)\), la función que representa el programa.
Por lo tanto, para ver cómo demodular una señal FM, tenemos que ver qué recibimos cuando sintonizamos una frecuencia distinta de la portadora. Supongamos que la portadora es una senoidal de amplitud constante \(A\) y frecuencia constante \(f_c + f_\delta\), siguiendo la fórmula \(A\cos(2\pi(f_c+f_\delta)t + \varphi)\). Esta senoidal tiene dos componentes complejas, una de frecuencia \(-f_c-f_\delta\) y otra de frecuencia \(f_c+f_\delta\). Sintonizando la frecuencia \(f_c\), el sintonizador nos proporciona una señal con dos componentes: una de frecuencia \(-2f_c-f_\delta\) y otra de frecuencia \(f_\delta\). La frecuencia de la primera componente es superior a la frecuencia umbral de los filtros paso bajo, con lo que nos quedamos con sólo la componente de frecuencia \(f_\delta\), que sigue la fórmula \(\frac{A}{2}e^{i(2\pi f_\delta t + \varphi)}\). Por lo tanto, al sintonizar una señal de frecuencia constante distinta de la frecuencia sintonizada, el resultado es una onda compleja cuya frecuencia es la diferencia entre la frecuencia de la señal y la frecuencia sintonizada, y cada muestra representa un valor de esta onda para cada instante de tiempo \(t\).
Si la diferencia en frecuencia no es constante sino que es una frecuencia variable \(f_\delta(t)\), el resultado es parecido: el resultado es una onda compleja de frecuencia variable \(f_\delta(t)\). Para obtener la señal original tenemos que estimar el valor de \(f_\delta(t)\) en cada instante en el tiempo y aplicar la fórmula \(p(t) = \frac{f_\delta(t)}{f_\Delta}\). El quid del asunto está en cómo se estima esta frecuencia.
El método más sencillo es, simplemente, calcular el ángulo del número complejo contenido en cada muestra y después calcular la diferencia entre los ángulos de dos muestras contiguas y dividir el resultado por el intervalo de tiempo entre dos muestras. El resultado es la frecuencia angular en radianes/segundo, que podemos entonces dividir por la desviación de frecuencia máxima en radianes/segundo para obtener el valor de \(p(t)\) en cada instante. Parece demasiado simple, pero este método funciona extraordinariamente bien, aunque en la práctica lo que hacemos es dividir la segunda muestra por la primera y calcular el ángulo del resultado. Lamentablemente, el descodificador no nos proporciona números complejos en forma polar, que son fáciles de dividir y cuyo ángulo es trivial de obtener, sino que nos los da en forma cartesiana, en la que estas operaciones son más complicadas. Afortunadamente, podemos usar un par de atajos para realizar estas operaciones más rápido.
En teoría, primero tenemos que dividir los dos números complejos \((a+bi)\) y \((c+di)\) y luego obtener el ángulo calculando el arco tangente de la parte imaginaria del resultado dividida por la parte real. Para dividirlos usaríamos la fórmula \(\frac{(ac+bd)+i(bc-ad)}{c^2-d^2}\), lo cual nos obligaría a hacer 6 multiplicaciones, 2 divisiones y 3 sumas. Sin embargo, como vamos a dividir la parte real e imaginaria de este resultado, no necesitamos calcular el divisor, ya que desaparece al hacer la división, así que sólo necesitamos calcular \((ac+bd)\) y \((bc-ad)\), lo que nos deja con 4 multiplicaciones y 2 sumas.
Calcular el arco tangente también es una operación bastante lenta. He visto que algunos programas que demodulan FM simplemente tragan con esta lentitud y usan la función arco tangente, pero yo he utilizado una fórmula que aproxima el arco tangente usando un polinomio de grado 3. Esta aproximación es bastante buena para mis propósitos (0.1%, si no recuerdo mal) y es mucho más rápida de calcular, con lo que al programa le queda más tiempo para demodular señales, filtrarlas y hacer otras operaciones necesarias.
Y así, calculando la diferencia de ángulo entre dos muestras consecutivas, multiplicándola por la frecuencia de muestreo y dividiéndola por la velocidad angular de la desviación máxima, es como el programa obtiene cada uno de los valores correspondientes al programa emitido \(p(t)\). Ahora, en principio, podríamos pasar las muestras de \(p(t)\) a la tarjeta de sonido y escuchar la radio. Sin embargo, el programa de una emisora FM no es tan simple, sino que contiene información extra para implantar cositas como stereo y RDS. Como este artículo se me ha quedado ya un poco largo, en el próximo artículo explicaré cómo se demodula una señal FM stereo.