En este artículo comento algunas de las cosas que se pueden hacer con números complejos. Hay dos formas de representar un número complejo: forma cartesiana y forma polar. Algunas operaciones con números complejos son más fáciles en forma polar y otras lo son en forma cartesiana, y este artículo se centra en la forma polar y en lo útil que es para hacer procesamiento de señales, que es un tema en el que estoy interesado últimamente.
Voy a comenzar hablando de planos. Imaginad que marco un punto \((a,b)\) en un plano cartesiano. Siempre es posible trazar una línea desde el origen de coordenadas \((0,0)\) hasta el punto \((a,b)\). Esa línea tendrá una longitud \(r\) y tendrá cierto ángulo \(\varphi\) respecto del eje \(x\), como podéis ver en el dibujito explicativo.
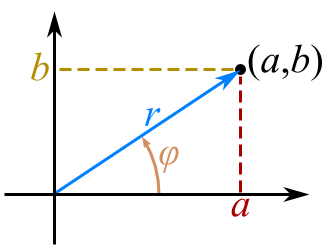
Todo punto \((a,b)\) tiene su longitud \(r\) y su ángulo \(\varphi\) y viceversa, así que tanto da representar un punto utilizando sus coordenadas cartesianas como utilizando longitud y ángulo; esto último se llama “coordenadas polares”. Para hallar \(a\) y \(b\) dados \(r\) y \(\varphi\) sólo es necesario utilizar trigonometría básica y calcular \(a = r\cos{\varphi}\) y \(b = r\sin{\varphi}\). Si queremos hacer el cálculo inverso y hallar \(r\) y \(\varphi\) para un punto \((a,b)\) dado, los cálculos necesarios son \(r = \sqrt{a^2+b^2}\) y \(\varphi = \mathrm{atan2}(b,a)\).
Ahora regresemos a los números complejos, y veamos qué valor tiene un número complejo \(re^{i\varphi}\). Utilizando la fórmula de Euler tenemos que \(re^{i\varphi} = r\cos{\varphi} + ir\sin{\varphi} = a+bi\). Por lo tanto, \(a = r\cos{\varphi}\) y \(b = r\sin{\varphi}\), que son exactamente las mismas fórmulas que acabamos de ver que sirven para convertir de coordenadas polares a cartesianas. Por lo tanto, también podríamos hacer la operación inversa y, usando las fórmulas para convertir de coordenadas cartesianas a polares, calcular los valores de \(r\) y \(\varphi\) para un número complejo \(a+bi\) que hacen que \(a+bi = re^{i\varphi}\).
Todo esto significa que un número complejo representa un punto en un plano, y que, igual que los puntos del plano se pueden representar en coordenadas cartesianas \((a,b)\) o polares \(r\) y \(\varphi\), un número complejo también se puede representar en forma cartesiana \(a+bi\) o en forma polar \(re^{i\varphi}\).
Seguramente os preguntaréis por qué no bastaba con tener una sola forma de representar los números complejos, y para qué queremos dos. La cuestión es que algunas operaciones son más sencillas de hacer en forma polar que en forma cartesiana. Por ejemplo, para multiplicar dos números complejos en forma cartesiana la operación es:
\[(a_1+b_1i)(a_2+b_2i) = (a_1a_2-b_1b_2)+(a_1b_2+b_1a_2)i \]
¡Vaya atracón de multiplicaciones y sumas! Sin embargo, multiplicar dos números complejos en forma polar sólo requiere una suma y un producto, y nada más:
\[r_1e^{i\varphi_1}r_2e^{i\varphi_2} = r_1r_2e^{i(\varphi_1+\varphi_2)} \]
Y aquí podéis ver otra interesante propiedad de los números complejos: al multiplicar dos números complejos, sus ángulos se suman. Esto nos permite “girar” un número complejo, es decir, cambiar su ángulo: simplemente lo multiplicamos por otro número complejo de la forma \(e^{i\alpha}\) para “girarlo” un ángulo \(\alpha\), y listo.
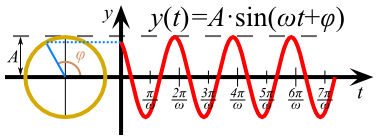
“¿Y por qué a Jacobo le parece interesante esta propiedad?”, os preguntaréis. Muy simple: esta propiedad es muy útil para hacer procesamiento digital de señales. Y para ver por qué es util, antes tenemos que ver una señal. En el dibujo de la derecha podéis ver la “señal” más típica del mundo: una onda senoidal de amplitud y frecuencia fijas. Uno puede describir esta onda como una función respecto del tiempo \(t\) mediante la expresión \(y(t) = A\sin(\omega t + \varphi)\), donde \(A\) es la amplitud, \(\omega\) es la frecuencia angular, y \(\varphi\) es la fase de la señal. La amplitud controla cómo de amplias son las oscilaciones (valga la redundancia), la frecuencia controla cuántas oscilaciones hay por unidad de tiempo, y la fase es la posición de la oscilación cuando \(t=0\).
Si le preguntáis a alguien que se dedique al procesamiento de señales, os dirá que sí, que el dibujo de la derecha es correcto, pero que en realidad el seno y el coseno de un ángulo son la suma o la diferencia de dos números complejos: por un lado, \(\cos{\varphi} = \frac{1}{2}(e^{i\varphi}+e^{-i\varphi})\) y por el otro lado, \(\sin{\varphi} = \frac{1}{2}i(e^{-i\varphi}-e^{i\varphi})\). Esto significa que se pueden tratar señales como la de arriba usando números complejos, y que, de hecho, la señal más elemental no es la onda senoidal de arriba, sino una onda compleja como \(y(t) = Ae^{i(\omega t + \varphi)}\), que se puede manipular muy fácilmente utilizando otros números complejos.
Vamos a ver qué podemos hacer con \(y(t) = Ae^{i(\omega t + \varphi)}\). Una cosa que podemos hacer es variar su fase. Para hacerlo no tenemos más que multiplicar la función por un número complejo \(e^{i\alpha}\), y el resultado será \(y_1(t) = Ae^{i(\omega t + (\varphi + \alpha))}\). La frecuencia angular sigue siendo \(\omega\), pero ahora la fase es \(\varphi+\alpha\).
Otra cosa que podemos hacer es cambiar su frecuencia. Para ello tenemos que multiplicar la onda por otra onda de amplitud 1 y de la frecuencia que queramos sumar a la onda original. Por ejemplo, si queremos sumar \(\beta\) radianes/segundo a la frecuencia, multiplicaremos la señal por \(e^{i\beta t}\), lo que nos da \(y_2(t) = Ae^{i((\omega + \beta)t + \varphi)}\). Ahora la fase sigue siendo \(\varphi\), pero la frecuencia es \(\omega+\beta\).
Una tercera cosa que podemos hacer es cancelar su frecuencia completamente, multiplicando la señal por otra de la misma frecuencia, pero negada, para convertirla en una onda de frecuencia 0 (es decir, en un valor constante, que no varía con el tiempo). El valor resultante es un número complejo que nos permite conocer la amplitud y la fase de la onda. Como ejemplo, multiplicamos la señal de arriba por \(e^{-i\omega t}\), lo que nos da \(Ae^{i(\omega t+\varphi)}e^{-i\omega t} = Ae^{i((\omega - \omega)t+\varphi)} = Ae^{i\varphi}\).
Y ahora es cuando voy a escribir dos cosas súper importantes, con las que terminaré el artículo de hoy. La primera es que igual que una onda senoidal se puede representar como la suma de dos ondas complejas, cualquier señal se puede representar como una suma de infinitas ondas complejas, cada una con su propia amplitud, frecuencia y fase. No lo voy a demostrar, pero os prometo que es verdad. La segunda cosa súper importante es que es posible calcular todas esas amplitudes y fases para cada una de las frecuencias que componen una señal. Se pueden obtener para una sola frecuencia haciendo lo que hicimos arriba: multiplicando la señal por una onda compleja de frecuencia negativa y examinando el número resultante. También se puede hacer al por mayor, para todas las frecuencias al mismo tiempo, utilizando la Transformada de Fourier (no la de Fournier; ésa es otra). Pero la Transformada de Fourier es un tema sobre el que se podrían escribir páginas y páginas, y este artículo ya es bastante largo, así que mejor lo dejaré para otro día.