En el último artículo dije que había dos cosas súper importantes, hice un breve resumen de ellas e inmediatamente después terminé el artículo sin explicarlas mejor. Qué mala educación por mi parte. En este artículo no sólo voy a corregir ese paso en falso, sino que también explicaré otras cosas que también os resultarán interesantes (espero).

La primera idea súper importante con la que acabé el artículo es que cualquier señal se puede representar como una suma de infinitas ondas complejas, cada una con su propia amplitud, frecuencia y fase. Por ejemplo, una senoidal es la suma de dos ondas complejas con frecuencias y fases opuestas, y cada una de la mitad de amplitud que la senoidal. (En lenguaje matemático, \(\cos(\omega t + \varphi) = \frac{1}{2}(e^{i(\omega t + \varphi)} + e^{-i(\omega t + \varphi)})\), que queda mucho más corto y claro. Y por esto, filliños, hay que saber leer expresiones matemáticas).

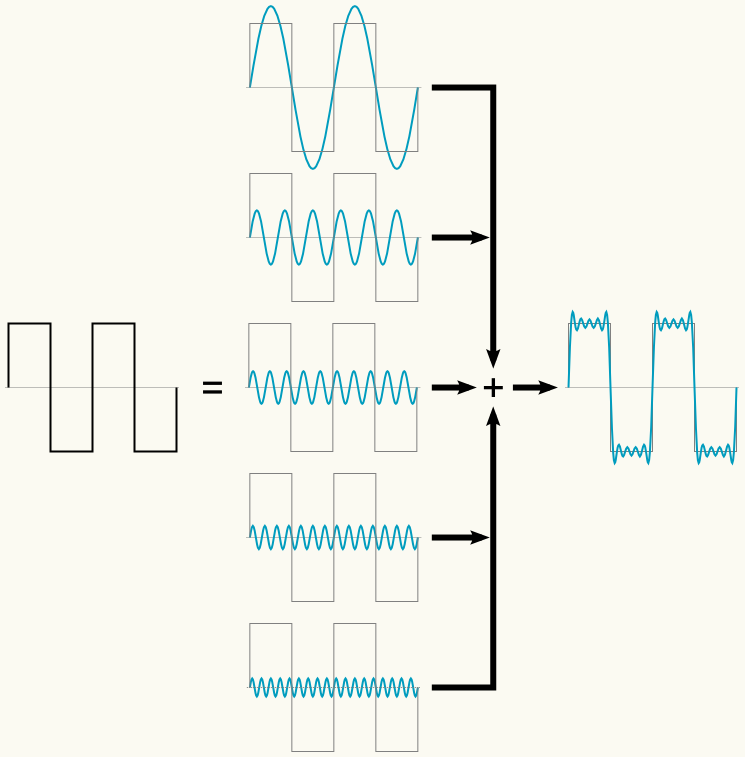
Esto es cierto incluso para las formas de onda más complicadas; por ejemplo, en la ilustración superior podéis ver cómo una onda cuadrada se puede descomponer en una suma de senoidales. Sólo he puesto unas cuantas, porque no tengo suficiente sitio para poner infinitas, pero incluso con sólo las cinco que hay ya véis que la forma de onda resultante se parece bastante a la onda cuadrada original, y si añadiéramos más se parecería aún más todavía, hasta llegar al momento en que tendríamos infinitas ondas y una perfecta copia de la onda cuadrada original.

Y dicho esto llegamos al segundo punto súper importante de la anterior historia: las magnitudes y fases de todos esos componentes se pueden calcular para cualquier forma de onda empleando la transformada de Fourier. Muchas veces se representa la transformada de Fourier de una onda mediante una gráfica que relaciona cada frecuencia con la correspondiente magnitud del componente que presenta esa frecuencia. Debajo podéis ver una versión extremadamente simplificada de una de esas gráficas, correspondiente a una grabación de mi voz diciendo “Hola, soy Jacobo”. En estas gráficas, el eje horizontal indica la frecuencia, con 0 en el centro, frecuencias positivas a la derecha, y frecuencias negativas a la izquierda; el eje vertical representa la magnitud de cada componente en frecuencia. Por lo tanto, la magnitud de las frecuencias inferiores a 1000 Hz es bastante alta, y a partir de ahí va bajando, aunque con picos alrededor de los 7000 Hz y los 12000 Hz.

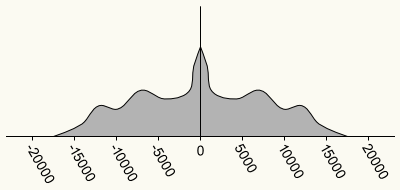
(A todo esto, tal vez os preguntéis por qué el diagrama es simétrico respecto de la frecuencia 0. Esto es, a grandes rasgos, porque las ondas sonoras son sumas de senoidales, que tienen una componente de frecuencia negativa y otra de frecuencia positiva que tienen la misma magnitud. Cada vez que tengamos señales que se pueden representar usando números reales tendremos una transformada de Fourier simétrica. Si la transformada es asimétrica, la señal es compleja).

Al resultado de la transformada de Fourier también se le puede aplicar una “transformada inversa” para recuperar la señal original. Esto significa que tanto nos da representar una señal como una función cuyo valor varía con el tiempo que representarla como una serie de componentes en frecuencia, porque podemos convertirla a la otra representación fácilmente. Los que trabajan en este campo hablan de “dominio del tiempo” y “dominio de la frecuencia”, respectivamente, para referirse a estas dos formas de representar una señal.

En el mundillo del tratamiento digital de señales se utiliza muchísimo la transformada de Fourier. Ahora bien, el tratamiento digital de señales se hace empleando ordenadores, que son aparatos a los que no se les da nada bien tratar con infinitos elementos. Afortunadamente, no es necesario hacerlo, debido a la manera en que un ordenador procesa una señal.

Conceptualmente, una señal es un valor que varía de forma continua; es decir, la onda oscila, y podemos ver el valor de esa oscilación en cualquier instante en el tiempo. Sin embargo, un ordenador utiliza muestreo; el ordenador sólo guarda los valores de la señal a intervalos regulares, así que sólo podemos ver los valores de esa oscilación para los instantes en los que el ordenador capturó una muestra.

Se suelen utilizar frecuencias de muestreo bastante elevadas. Por ejemplo, un CD tiene guardadas 44100 muestras por segundo, y la tarjeta de sonido de un ordenador moderno puede almacenar 48000 muestras por segundo, aunque los hay que pueden capturar 192000. Estas frecuencias de muestreo son así de elevadas porque resulta que la frecuencia de muestreo limita la máxima frecuencia que puede contener la señal muestreada: esta frecuencia máxima es la mitad de la frecuencia de muestreo. Así, por ejemplo, la máxima frecuencia del sonido guardado en un CD es 22050 Hz.

Por lo tanto, cuando un ordenador calcula la transformada de Fourier de una señal muestreada con una frecuencia de muestreo \(S\), no obtiene infinitas frecuencias, sino sólo frecuencias entre \(\frac{-S}{2}\) y \(\frac{S}{2}\). Es más: el número de componentes en frecuencia es igual al número de muestras. Por lo tanto, el ordenador no necesita en ningún momento tratar con infinitos elementos. ¡Viva!

Para un ordenador, una señal no es más que una lista de números, a la que se pueden aplicar muchísimas operaciones matemáticas. Y, por supuesto, al aplicar esas operaciones a la lista de muestras en el dominio del tiempo, también se afecta a la señal en el dominio de la frecuencia. Veamos unos ejemplos.

Una posible operación es, simplemente, multiplicar cada muestra por una constante real, por ejemplo \(2\). El resultado es que ahora la señal tiene el doble de amplitud y todos los componentes en frecuencia también tienen el doble de magnitud que antes. Fácil.

Otra posible operación es multiplicar cada muestra por un número complejo constante de la forma \(e^{i\varphi}\). El resultado es que a la fase de todos los componentes en frecuencia se le ha sumado un ángulo \(\varphi\). Es así como se puede modificar fácilmente la fase de una señal.

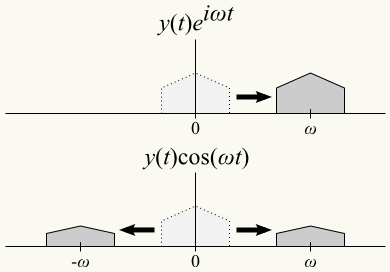
Otra interesante operación que se puede hacer es generar una señal compleja de la forma \(e^{i\omega t}\) y multiplicar cada muestra de la señal original por la correspondiente muestra de la señal compleja (la primera muestra por la primera muestra, la segunda por la segunda, etc.) El resultado es que cada componente en frecuencia se ha desplazado \(\omega\) radianes por segundo (1 Hz son \(2\pi\) radianes/segundo) y, por lo tanto, la señal entera está desplazada en frecuencia. La parte de arriba del dibujo superior lo muestra de forma gráfica: la señal original \(y(t)\), que estaba centrada en la frecuencia 0, la hemos multiplicado por \(e^{i\omega t}\), y ha pasado a estar centrada en la frecuencia \(\omega\).

La parte de abajo del dibujo muestra una operación similar que se puede hacer sin utilizar números complejos. Esta operación consiste en generar una senoidal de la forma \(cos(\omega t)\) y multiplicar cada muestra de la señal original por la correspondiente muestra de la senoidal. La señal resultante contiene dos copias de la señal original, cada una con la mitad de la amplitud original, y una de ellas desplazada \(\omega\) radianes por segundo y la otra desplazada \(-\omega\) radianes por segundo. Si ahora multiplicamos esta señal por otra senoidal con otra frecuencia distinta, \(\cos(\omega_1 t)\), cada una de las señales volvería a desdoblarse, y acabaríamos teniendo cuatro señales de la cuarta parte de la amplitud original, centradas en \(\omega+\omega_1\), \(\omega-\omega_1\), \(-\omega+\omega_1\) y \(-\omega-\omega_1\).

Estoy llegando al final de este artículo, y en este punto os estaréis preguntando para qué sirve todo esto. Pues bien: esto se utiliza para transmitir señales por radio. A grandes rasgos, la idea es que cada emisora de radio tiene una frecuencia asignada (llamémosla \(\omega_c\)), y sus transmisiones tienen que estar centradas en esa frecuencia. Lo que hacen es tomar la señal a transmitir, multiplicarla por \(\cos(\omega_c t)\) para centrarla en las frecuencias \(\omega_c\) y \(-\omega_c\), amplificarla y enviarla a la antena.

Para recibir la señal, el receptor de radio necesita desplazar la señal hasta una frecuencia intermedia (llamémosla \(\omega_i\)), así que multiplica las señales eléctricas procedentes de la antena por una senoidal de frecuencia \(\omega_c-\omega_i\) (obteniendo señales centradas en \(\omega_i\) y \(2\omega_c-\omega_i\), y también en las correspondientes frecuencias negativas) y luego utiliza un filtro para eliminar todas las señales excepto las que estén en una banda de frecuencias centrada en \(\pm\omega_i\). Luego aplica un circuito detector, obtiene la señal original, la amplifica y la envía al altavoz o los auriculares. ¡Fácil!

Por supuesto, estos dos últimos párrafos no son del todo ciertos, pero de momento esa explicación servirá. En el próximo artículo, Dios mediante, explicaré cómo un ordenador puede utilizar un receptor de TDT para recibir y demodular radio FM.