¿Recordáis cómo se resuelve una raíz cuadrada con lápiz y papel?
[Actualización 11 de diciembre de 2011: si no lo recuerdas y has llegado aquí buscando cómo hacerlo, tengo otro artículo con la explicación.]
[Actualización 5 de abril de 2020: mientras pasaba los artículos antiguos a la nueva página web he leído esta página y me he dado cuenta de que muy complicada de entender, así que he decidido reescribirla. Con un poco de suerte, 11 años después, puedo escribir algo más fácil que entonces.]
Es posible que necesite recordaros a algunos de vosotros qué es una raíz cuadrada. Al multiplicar un número por sí mismo, estás calculando su cuadrado. La operación inversa —es decir, a partir de un número obtener otro cuyo cuadrado es el número original— es la raíz cuadrada. Por lo tanto, el cuadrado de 5 es 25, ya que \(5 \times 5=25\), y la raíz cuadrada de 16 es 4 ya que \(16=4 \times 4\).
Por supuesto, es muy fácil calcular la raíz cuadrada de ciertos números, como 4, 9, 16 o 25. No obstante, no es tan fácil calcular las raíces cuadradas de otros números como el 529. Para hacerlo, uno normalmente tomaría lápiz y papel y empezaría a hacer dibujitos, siguiendo unos pasos similares a los que se representan en la siguiente figura:
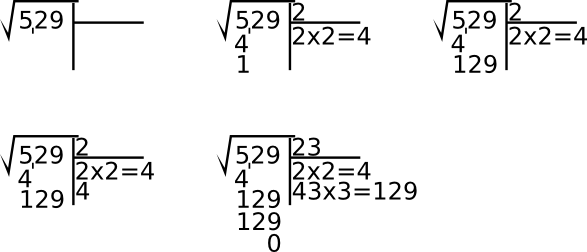
Me tomaría mucho tiempo y espacio realizar un resumen del método, así que simplemente podéis leerlo en otro artículo y entretanto yo seguiré adelante con esta historia.
La pregunta que algunos nos hemos hecho en algún momento es cómo funciona el método. Es bastante complicado: tenemos que agrupar los dígitos dos a dos y multiplicar los resultados parciales por dos, añadir el dígito al final y multiplicar el resultado por el mismo dígito y… Al final parece casi un milagro que obtengamos la respuesta correcta.
El sistema se basa en que el cuadrado de la suma de dos números es igual a la suma del cuadrado del primer número, el cuadrado del segundo número y el doble del producto de ambos números. Por ejemplo, el cuadrado de la suma de 4 y 7 es \(4^2 + 7^2 + 2 \times 4 \times 7 = 16 + 49 + 56 = 121\), que es, efectivamente, el cuadrado de 11.
Podemos descomponer un número de dos cifras en la suma de un número de una cifra y otro número que es múltiplo de 10. Por ejemplo, \(39=30+9\), o \(74=70+4\). Esto nos permite calcular el cuadrado de éstos números de dos cifras muy fácilmente usando el resultado de antes. Por ejemplo, \(39^2 = (30 + 9)^2 = 30^2 + 9^2 + 2 \times 30 \times 9 = 900 + 81 + 540 = 1521\).
El método para resolver la raíz cuadrada con lápiz y papel es lo mismo de arriba, pero dado la vuelta. Queremos buscar dos números: uno que es un múltiplo de 10 y otro de una cifra, que el cuadrado de su suma es igual al número que tenemos.
Vamos a buscar la raíz cuadrada de 529 y así podéis comparar la explicación que viene con los pasos seguidos en la solución que aparece arriba. Para ello, tenemos que buscar dos cifras por las que podemos sustituir las letras “\(a\)” y “\(b\)” para que la siguiente igualdad sea cierta:
\[529 = a0^2 + b^2 + 2 \times a0 \times b \]
El primer paso es buscar el valor de “\(a\)”. Este valor tiene que ser el más alto tal que el cuadrado de \(a0\) sea igual o menor que 529. O, dicho de otra forma, el cuadrado de \(a\) tiene que ser igual o menor que 5. El número más alto que cumple esto es 2, así que sustituyo \(a\) por 2 en la igualdad, lo que me da:
\[529 = 20^2 + b^2 + 2 \times 20 \times b = 40 + b^2 + 40 \times b \]
Para hacer esta suma algo más fácil puedo restar 40 en ambos lados de la suma y operar un poco con \(b^2\) y \(40 \times b\), con lo que me queda:
\[129 = b^2 + 40 \times b = (40 + b) \times b = 4b \times b \]
Como podéis ver, esto se corresponde exactamente con ese paso tan extraño de “buscar la cifra, añadirla al final y luego multiplicar por esa misma cifra”. Parece que el número 3 encaja bien en lugar de \(b\), ya que \(43 \times 3 = 129\), por lo que ahora tenemos el valor de nuestras cifras \(a\) y \(b\), que nos dan el número 23.