Un día se me ocurrió publicar un articulito sobre el fundamento matemático del método para calcular raíces cuadradas usando lápiz y papel. Desde entonces me llega un montón de visitas de gente que quiere saber cómo calcular una raíz cuadrada (supongo que les da igual por qué funciona el método si no saben cómo emplearlo, ¿no?). Por lo tanto, he decidido escribir este artículo explicativo.
Para empezar, vamos a ver cómo calcular la raíz cuadrada de un número de una o dos cifras. Por ejemplo, calculemos la raíz cuadrada de 71:
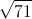
Esto es fácil: simplemente tenemos que hallar el número más alto, del 0 al 9, que multiplicado por si mismo nos dé 71 o menos. En este caso, el número que buscamos es 8, ya que 8x8=64, que es inferior a 71, y 9x9=81, que es superior a 71. Además, la operación tiene un “resto” que vale 7, ya que 71-8x8=7. Todo esto lo escribimos de esta manera:
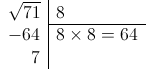
Fácil, ¿no?
Pues ahora vamos a ver cómo se calcula la raíz cuadrada de un número de más de dos cifras. Por ejemplo, el 71.492:
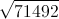
El primer paso consiste en dividir el número en grupos de dos dígitos, comenzando por la derecha:
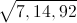
A continuación, calculamos la raíz cuadrada del grupo de más a la izquierda:
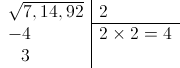
En este caso hemos calculado la raíz cuadrada de 7, que es 2 con un resto de 3.
A continuación “bajamos” el siguiente grupo de dos dígitos y lo ponemos a la derecha del resto:
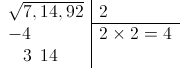
En el siguiente paso multiplicamos nuestra solución parcial por 2 (siempre por 2) y ponemos el resultado (4) en una nueva fila de la columna de la derecha:
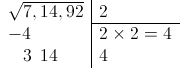
Ahora viene la parte más complicada del cálculo. Tenemos que buscar un dígito de 0 a 9 para añadir a la derecha del 4, lo cual nos dará un número de dos cifras. Ese número de dos cifras, multiplicado por el dígito que hemos buscado, nos dará un número que tiene que ser igual o inferior a 314, que es el número que tenemos después de “bajar” el siguiente grupo de cifras. El dígito más alto que encontremos será la siguiente cifra de la solución.
Veamos un dibujo para hacerlo más claro. Imaginad que “X” es un dígito de 0 a 9 y que “ABC” es el resultado de multiplicar “4X” por “X”:
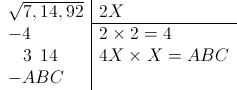
En este caso, el dígito que buscamos es 6, porque 46x6=276, que es inferior a 314, y 47x7=329, que se pasa de 314:
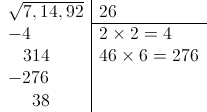
El resto es 38.
Ahora tenemos que, como antes, bajar el siguiente grupo de cifras y también multiplicar la solución parcial por 2 y añadir el resultado a la columna de la derecha:
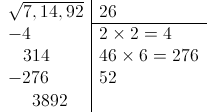
Y, como antes, tenemos que buscar un dígito, concatenarlo al “52”, multiplicarlo por el resultado, y procurar que el resultado sea igual o inferior a 3892:
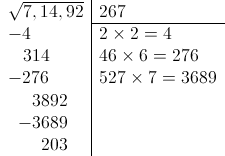
Y, como podéis ver, la raíz cuadrada de 71492 es 267, con un resto de 203. Podemos comprobarlo fácilmente, calculando 267x267=71289, y 71492-71289=203.
Fácil, ¿no?
Algunos os preguntaréis cómo se pueden calcular las cifras decimales de la raíz cuadrada. Es decir, si usamos una calculadora, ésta nos dirá que la raíz cuadrada de 71492 es 267,3798… ¿cómo se pueden calcular estas cifras decimales con lápiz y papel?
La respuesta es muy simple: sólo tenéis que “bajar” grupos de dos ceros y seguir calculando la raíz cuadrada hasta que os canséis. Por ejemplo, aquí veis cómo he calculado las dos primeras cifras decimales:

Otra pregunta que algunos os haréis es: ¿cómo se calcula la raíz cuadrada si el número que nos dan tiene decimales? La respuesta es simple: cuando dividáis el número en grupos de dos cifras, en lugar de empezar por la derecha, empezad por la coma decimal. Si el grupo de más a la derecha se queda con una sola cifra, completadlo con un cero. Después, simplemente calculad la raíz cuadrada como siempre, acordándoos de poner la coma en el resultado cuando alcancéis la coma en el número original.
Y esto es todo de momento. Espero que esta explicación os haya sido útil y hayáis encontrado lo que buscábais.